Triángulo rectángulo

---

Triángulo rectángulo

Los triángulos rectángulos BAC, AHB y AHC tienen sus tres ángulos iguales. Ello permitirá la obtención de importantes Teoremas.

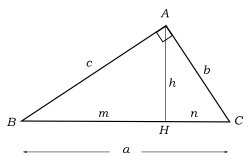
Triángulo rectángulo es aquel triángulo que tiene un ángulo recto. Los lados de éste se llaman catetos, y el tercer lado es la hipotenusa.

La altura h relativa a la hipotenusa, divide al triángulo rectángulo BAC en los triángulos AHB y AHC, ambos rectángulos en H.

Los triángulos BAC, AHB y AHC tienen sus tres ángulos iguales:

1. Todos tienen un ángulo recto.
2. Los ángulos agudos ABH y HAC, así como HCA y HAB, son iguales por tener sus lados perpendiculares.
3. Los ángulos B y C son comunes para los tres triángulos.

Consecuentemente hemos obtenido tres triángulos rectángulos semejantes.

Teorema del cateto

Por la semejanza entre los triángulos AHB y BAC tenemos que

${\frac {c}{m}}={\frac {a}{c}}$

$c^{2}=a\,m$

De la semejanza entre los triángulos AHC y BAC, tenemos análogamente que

${\frac {b}{n}}={\frac {a}{b}}$

$b^{2}=a\,n$

Las expresiones obtenidas son el teorema del cateto: en un triángulo rectángulo cada cateto es media proporcional entre la hipotenusa y su proyección sobre ella.

Teorema de la altura

Por la semejanza entre los triángulos AHB y AHC nos resulta:

${\frac {h}{m}}={\frac {n}{h}}$

es decir,

$h^{2}=m\,n$

expresión del teorema de la altura: en un triángulo rectángulo la altura relativa a la hipotenusa es media proporcional a los segmentos que determina en ella.

Teorema de Pitágoras

El teorema del cateto y el Teorema de Pitágoras. Conforme al teorema del cateto, los cuadrados de lados b y c tienen la misma superficie que los rectángulos de igual color en el cuadrado de lado a. El teorema de Pitágoras se hace evidente.

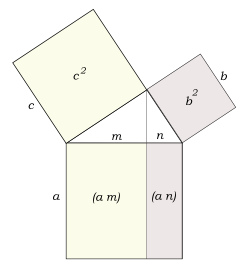
En un triángulo rectángulo el cuadrado construído sobre la hipotenusa es igual a la suma de los cuadrados construídos sobre los catetos.

Algebraicamente:

$a^{2}\,=\,b^{2}+c^{2}$

Podemos demostrarlo con el teorema del cateto.

$b^{2}=a\,n$

$c^{2}=a\,m$

sumando,

$b^{2}+c^{2}\,=\,an+am$

sacando factor común,

$b^{2}+c^{2}\,=\,a(n+m)$

pero $(n+m)\,=\,a$, con lo que efectivamente:

$b^{2}+c^{2}\,=\,a^{2}$

Esta demostración pudo haber sido una de las dadas por Pitágoras a su teorema.