Altura de un triángulo

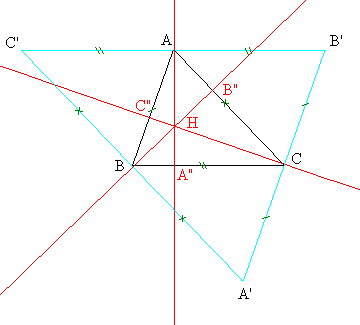
Sea ABC un triángulo cualquiera. Una altura del triángulo es una recta que pasa por un vértice y que es perpedicular al lado opuesto.

En la figura, las tres alturas son (AA"), (BB") y (CC"). Según el contexto, también se puede llamar alturas los segmentos [AA"], [BB"] y [CC"], y sus longitudes reciben la misma apelación.

El uso más común de la altura, como longitud, es el siguiente: el área de un tríangulo es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac {h \cdot b} 2 }

, donde b es una

base o sea la longitud de un lado, y h la altura correspondiente.

En la figura, el área es :

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathfrak{A} = \frac {BC \cdot AA''} 2 = \frac {AB \cdot CC''} 2 = \frac {AC \cdot BB''} 2 }

.

Está fórmula se demuestra dibujando un rectángulo cuya área es doble del área el triángulo, con la misma base y la misma altura.

Teorema:

Las tres alturas se cortan en un único punto, llamado ortocentro del triángulo (H en él gráfico).

Prueba:

Se trazan las rectas paralelas a los lados y que pasan por los vértices opuestos. Se obtienen así las rectas (A'B'), (B'C') y (A'C'). El triángulo A'B'C' es dos veces mayor que ABC, y los puntos A, B y C son los centros de sus lados. Esto se demuestra observando que ACBC', ABCB' y BACA' son por construcción paralelogramos. Las alturas de ABC aparecen entonces como las mediatrices de A'B'C', que son concurrentes en el centro del círculo circunscrito a A'B'C'.

Otra propiedad: H pertenece a la Recta de Euler