Tridimensional

En geometría y Análisis matemático, un objeto o ente es tridimensional si tiene tres dimensiones. Es decir cada uno de sus puntos puede ser localizado especificando tres números dentro de un cierto rango.

Espacio físico tridimensional

En un Espacio euclídeo‏‎ convencional un objeto físico finito está contenido dentro de un ortoedro mínimo, cuyas dimensiones se llaman ancho, Largo y profundidad. El espacio físico a nuestro alrededor es tridimensional a simple vista. Sin embargo, cuando se consideran fenómenos físicos como la gravedad, la Teoría de la relatividad nos lleva a que el universo es un ente tetra-dimensional que incluye tanto dimensiones espaciales como el tiempo como otra dimensión. Diferentes observadores percibirán diferentes "secciones espaciales" de este espacio-tiempo por lo que el espacio físico es algo más complejo que un espacio euclídeo tridimiensional.

Además ciertas teorías físicas de tipo Kaluza-Klein como las diferentes versiones de la Teoría de cuerdas postula que existe un número adicional de dimensiones compactificadas, que sólo serían observables en experimentos con partículas altamente energéticas. En estas teorías algunas de las Interacciones fundamentales pueden ser explicadas de manera sencilla postulando dimensiones adicionales de un modo similar a como la relatividad general explica la gravedad. De hecho la propuesta original de Theodor Kaluza explicaba de manera unificada el Electromagnetismo y la gravedad postulando un universo de 5 dimensiones con una dimensión compactificada.

No se conoce con precisión qué razones físicas subyacen para que el número de dimensiones espaciales extensas (no-compactificadas) es igual a tres. Ehrenfest señaló que en cuatro o más dimensiones las órbitas planetarias cerradas por ejemplo no serían estables. También se sabe que existe una conexión entre la intensidad de un campo de fuerzas estático con simetría esférica que satisface el teorema de Gauss y la dimensión del espacio, un campo gravitatorio, electrostático o de otro tipo que cumpla con dichas condiciones para gradens distnacias debe tener una variación de la forma:

$\phi \varpropto {\frac {f}{r^{d-1}}},\qquad d\geq 3$

Donde:

$f\,$ es una magnitud extensiva que mida la capacidad de fuente para provocar el campo, para un campo gravitatorio coincide con la masa y para uno eléctrico con la carga.

$r\,$ es la distancia al "centro" de la fuente que crea el campo.

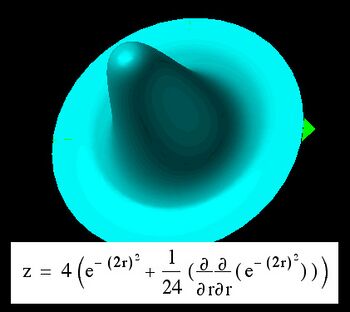
Ejemplos de formas tridimensionales

En geometría son tridimensionales las siguientes figuras geométricas:

• poliedro‏‎s de caras planas:
  • Pirámides
  • Cubo
  • prismas
• Superfices curvas:
  • Cilindro
  • Conos
  • Esfera o 3-esfera

Ya que todas ellas pueden ser embebidas en un espacio euclídeo de tres dimensiones. Sin embargo, hay que señalar que técnicamente la esfera, el cono o el cilindro son variedades bidimensionales (solo la cáscara) ya que los puntos interiores a ellos no son estrictamente parte de los mismos. Sólo por una abuso de lenguaje o extensión del mismo informalmente se habla de esferas, cilindros o conos incluyendo el interior de los mismos.

Por otra parte existe la hiperesfera tridimensional (3-variedad) pero no es la cáscara de una bola sino la compactificación de $\mathbb {R} ^{3}$ con un punto, así como la 2-esfera es para el plano euclídeo $\mathbb {R} ^{2}$.

Sistemas tridimensionales en ciencias naturales

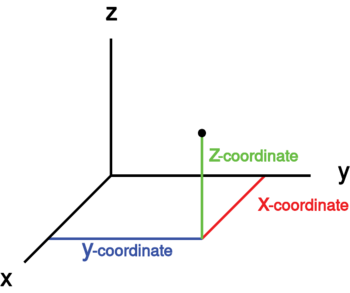
En química, se habla de sistemas tridimensionales cuando el enlace químico es igualmente intenso en las tres direcciones del espacio (por ejemplo, en el diamante). En magnetismo, se dice que el Ordenamiento magnético sólo es posible si el Acoplamiento magnético es tridimensional (se extiende en las tres direcciones del espacio). En matemáticas el sistema tridimensional se representa en el plano cartesiano con los ejes X, Y y Z. Por lo general en estas representaciones se manejan las formas geométricas de tres dimensiones como los cubos o las esferas.

Simulación 3D

Hoy en día es posible la simulación mediante cálculos basados en la proyección de entornos tridimensionales sobre pantallas bidimensionales, tales como monitores de ordenador o televisores. Estos cálculos requieren de una gran carga de proceso por lo que algunos Ordenadores y Consolas disponen de cierto grado de aceleración gráfica 3D gracias a dispositivos desarrollados para tal fin. Los ordenadores disponen de las llamadas tarjetas gráficas con Aceleración 3D. Estos dispositivos están formados con uno o varios procesadores (GPU) diseñados especialmente para acelerar los cálculos que suponen reproducir imágenes tridimensionales sobre una pantalla Bidimensional y de esta forma liberar de carga de proceso a la CPU o unidad de proceso central del ordenador.

Enlaces externos

• Video de imágenes en 3D reales, este es el futuro de los videojuegos
• Universidad donde estudiar Animación 3D. México

Referencias

Referencias e información de imágenes pulsando en ellas.