Pandeo

---

Pandeo

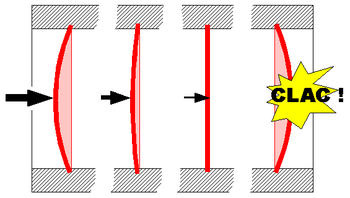El pandeo es un fenómeno de Inestabilidad elástica que puede darse en elementos comprimidos esbeltos, y que se manifiesta por la aparición de desplazamientos importantes transversales a la dirección principal de compresión.

En ingeniería estructural el fenómeno aparece principalmente en pilares y columnas, y se traduce en la aparición de una flexión adicional en el pilar cuando se halla sometido a la acción de esfuerzos axiales de cierta importancia. La aparición de flexión de pandeo limita severamente la resistencia en compresión de un pilar o cualquier tipo de pieza esbelta. Eventualmente, a partir de cierto valor de la carga axial de compresión, denominada carga crítica de pandeo, puede producirse una situación de inestabilidad elástica y entonces fácilmente la deformación aumentará produciendo tensiones adicionales que superarán la tensión de rotura, provocando la ruina del elemento estructural. Además del pandeo flexional ordinario existe el pandeo torsional o inestabilidad elástica provocado por un momento torsor excesivo.

Pandeo flexional

Los pilares y barras comprimidas de celosías puede presentar diversos modos de fallo en función de su esbeltez mecánica:

• Los pilares muy esbeltos suelen fallar por pandeo elástico y son sensibles tanto al pandeo local el propio pilar como al pandeo global de la estructura completa.
• En los pilares de esbeltez media las imperfecciones constructutivas como las heterogeneidades son particularmente importantes puediéndose presentar pandeo anelástico.
• Los pilares de gran esbeltez fallan por exceso de compresión antes de que los efectos del pandeo resulten importantes.

Pandeo local

El pandeo local es el que aparece en piezas o elementos aislados o que estructuralmente pueden considerarse aislados. En este caso la magnitud de la carga crítica viene dada según el caso por la fórmula de Leonhard Euler o la de Engesser. La carga crítica de Euler depende de la longitud de la pieza, del material, de su sección transversal y de las condiciones de unión, vinculación o sujeción en los extremos. Para una pieza que puede considerarse biarticulada en sus extremos la carga crítica de Euler viene dada por:

(1) $P_{crit}=\pi ^{2}{\frac {EI_{min}}{L^{2}}}=\pi ^{2}{\frac {EA}{\lambda ^{2}}}$

Siendo: P_crit, la carga crítica; E, Módulo de Young del material de que está hecha la barra; I_min, momento de inercia mínimo de la sección transversal de la barra; L, longitud de la barra y λ la esbeltez mecánica de la pieza. Cuando las condiciones de sujeción de los extremos son diferentes la carga crítica de Euler viene dada por una ecuación del tipo:

(2) $P_{crit}=\pi ^{2}{\frac {EI_{min}}{(\alpha L)^{2}}}\qquad {\begin{cases}\alpha =0.5&{\mbox{empotrdo, empotrado}}\\\alpha \approx 0.70&{\mbox{articulado, empotrado}}\\\alpha =2&{\mbox{libre, empotrado}}\end{cases}}$

Al producto $\alpha L\;$ se le llama longitud de pandeo.

Pandeo global

En una estructura compleja formada por barras y otros elementos enlazados pueden aparecer modos de deformación en los que los desplazamientos no sean proporcionales a las cargas y la estructura puede pandear globalmente sin que ninguna de las barras o elementos estructurales alcance su propia carga de pandeo. Debido a este factor, la carga crítica global de cierto tipo de estructuras (por ejemplo en entramados de cúpulas monocapa) es mucho menor que la carga crítica (local) de cada uno de sus elementos.

Ejemplo ilustrativo

El tipo de estructura más simple que presenta pandeo global para carga crítica diferente de la de sus elementos está formado por dos barras articuladas entre sí y a la cimentación, que se muestra en la figura.

Las ecuaciones que gobiernan el comportamiento de la estructura son:

• Ecuación de equilibrio:

$P=2Nsin(\theta -\Delta \theta )\,$

• Relación elástica entre acortamiento y esfuerzo axial:

$N=EA{\frac {\Delta L}{L}}$

• Relación geométrica de las configuraciones no-deformada y deformada:

$Lcos\theta =(L-\Delta L)cos(\theta -\Delta \theta )\,$

Donde: N, esfuerzo axial de cada una de las barras; ΔL, acortamiento sufrido por las barras para adoptar la configuración deformada; Δθ = θ-θ', es la diferencia de ángulos mostrada en la figura; E, móldulo de Young del material de las barras; A, área transversal de cada una de las barras; L, longitud inicial de cada una de las dos barras.

Substituyendo la segunda de las ecuaciones en la primera, despejando ΔL de la tercera y substituyendo su valor también su valor en la primera se llega a:

$P=2EA\left(1-{\frac {cos(\theta )}{cos(\theta -\Delta \theta )}}\right)sin(\theta -\Delta \theta )$

El valor de Δθ para el que se alcanza el máximo es precisamente la carga crítica global. Las cargas de pandeo global y local vienen dadas por:

$P_{crit,G}=2EA\left(1-cos^{\frac {2}{3}}\theta \right)\qquad \qquad P_{crit,L}={\frac {\pi ^{2}EI}{L}}$

Cada una estas cargas presenta modos de fallo diferentes en la estructura. De entre los dos posibles modos de fallo por pandeo ocurrirá el que presente un ángulo de aparición mayor donde estos ángulos vienen dados por:

$cos(\theta _{G})=cos^{\frac {1}{3}}(\theta )\qquad \qquad cos(\theta _{L})={\frac {\pi ^{2}EI}{L}}$

Pandeo torsional

En vigas de alas anchas, el pandeo flexional convencional puede ir acompañado de la aparación de una torsión de la sección, resultando un modo de fallo mixto conocido como pandeo torsional. El momento torsor crítico para el cual aparecería ese tipo de fallo viene dado por:

$M_{cr}={\frac {\pi }{\alpha L}}{\sqrt {\left({\frac {\pi EI_{m}}{\alpha L}}\right)^{2}I_{\omega }I_{m}+EI_{m}GJ}}$

Donde las nuevas magnitudes son:

$I_{m}\;$, es el momento de inercia mínimo en flexión.

$I_{\omega },J\;$, son respectivamente el Módulo de alabeo y el módulo de torsión.

$G\;$, el Módulo de elasticidad transversal.

Y el resto de magnitudes tienen el mismo significado que para el pandeo flexional puro. En piezas donde el momento de alabeo es despreciable puede usarse la expresión aproximada:

$M_{cr}\approx {\frac {\pi }{\alpha L}}{\sqrt {EI_{m}GJ}}$

Cálculo de cargas críticas

Curva elástica

Una manera de encontrar la carga crítica de una estructura consiste en presuponer la forma cualitativa en que esta pandeará, parametrizando esa forma cualitativa mediante varios parámetros incógnita. Introduciendo esa forma cualitativa en la ecuación de la curva elástica y buscando que la solución parametrizada satisfaga las condiciones de contorno cualitativas, que normalmente se refieren a desplazamientos y giros de los nudos de las barras de la estructura, se obtienen relaciones entre los parámetros incógnita introducidos. El valor de la carga crítica es precisamente el que hace que dichas relaciones se cumplan.

El método de Euler para barras aisladas es un ejemplo de uso de este método. Por ejemplo para determinar la carga de crítica de un pilar empotrado en su base y libre en el extremo tratamos de resolver la ecuación de la curva elástica bajo las siguientes condiciones:

${\frac {d^{2}w(h)}{dh^{2}}}+{\frac {Pw(h)}{EI}}={\frac {P\delta }{EI}}\qquad {\begin{cases}w'_{base}=0\\w_{sup}=\delta \end{cases}}$

La solución de esa ecuación, en función del parámetro de desplazamiento horizontal del pilar, resulta ser:

$w(h)=\delta \left[1-\cos \left(h{\sqrt {\frac {P}{EI}}}\right)\right]$

La condición de contorno en el extremo superior (donde h = H y w_sup = 0) sólo se cumple para ciertos valores de P, que cumplen:

$H{\sqrt {\frac {P_{n}}{EI}}}=(2n+1){\frac {\pi }{2}}\qquad n\in \mathbb {Z}$

El menor de estos valores es precisamente el valor aceptado para la carga crítica de Euler de un pila empotrado en su base y libre en su parte superior:

$P_{crit}=P_{0}={\frac {\pi ^{2}EI}{(2H)^{2}}}$

Métodos energéticos

Para estructuras de una cierta complejidad el método anterior resulta de muy difícil aplicación, ya que requiere integrar un número elevado de ecuaciones diferenciales para cada elemento lineal de la estructura.

Un método aproximado consiste en presuponer aproximadamente las deformaciones asociadas al pandeo, que satisfaga las condiciones de contorno en los extremos de las piezas, y en igualar la energía de deformación W_int con el trabajo exterior realizado por la fuerza que produce el fenómeno de pandeo W_ext durante la deformación, W_int = W_ext. Esas dos ecuaciones pueden escribirse en términos el campo de desplazamientos de los momentos flectores asociados. Para cada elemento lineal la energía de deformción y el trabajo exterior vienen dados por:

$W_{int}={\frac {1}{2}}\int _{0}^{L}EI\left[{\frac {d^{2}w(x)}{dx^{2}}}\right]^{2}dx\qquad \qquad W_{ext}={\frac {P_{crit}}{2}}\int _{0}^{L}\left[{\frac {dw(x)}{dx}}\right]^{2}dx$

Cuanto más ajustado sea el campo de desplazamientos supuesto w(x) mejores resultados da el método anterior.

Referencias

Referencias e información de imágenes pulsando en ellas.