Hiperboloide

---

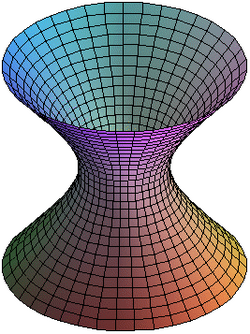
Hiperboloide

El hiperboloide es la superficie de revolución generada por la rotación de una hipérbola alrededor de uno de sus dos ejes de simetría.

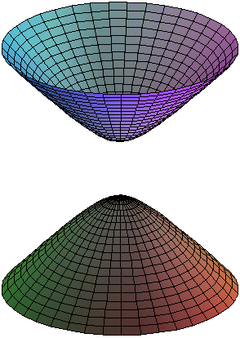
Estas superficies son de dos clases, como queda obvio en las figuras.

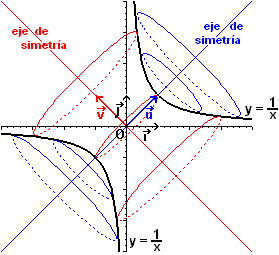
Para entenderlo mejor, se considera a continuación el caso de la hipérbola de referencia, cuya ecuación es

$y={\frac {1}{x}}$

, en el sistema de coordenadas

$(O,{\vec {i}},{\vec {j}})$

(ver el esquema suiguiente).

La revolución alrededor del eje de simetría rojo da un hiperboloide conexo, mientras que la rotación alrededor del eje azul, que atraviesa dos veces la hipérbola, da un hiperboloide de dos hojas.

Para hallar las ecuaciones de estas superficies, resulta más cómodo trabajar en el sistema de coordenadas $(O,{\vec {u}},{\vec {v}})$, cuyos ejes son los de simetría. Sean X e Y las coordenadas en este sistema, entonces tenemos la igualdad:

$X{\vec {u}}+y{\vec {v}}=x{\vec {i}}+y{\vec {j}}$

es decir

$X({\vec {i}}+{\vec {j}})+Y(-{\vec {i}}+{\vec {j}})=x{\vec {i}}+y{\vec {j}}$

, luego, identificando los coeficientes de sendos vectores:

$\left\{{\begin{matrix}X-Y=x\\X+Y=y\end{matrix}}\right.$ La ecuación inicial se escribe también xy = 1, es decir (X-Y)·(X+Y) = 1, luego: X² - Y² = 1.

Si se gira alrededor del eje de los Y, de Vector director

${\vec {v}}$

entonces se otorga a la tercera coordenada Z el mismo papel que a X, por tanto Z y X aparecen bajo la misma forma en la ecuación, concretamente precedido del signo «+»: X² + Z² - Y² = 1.
Del mismo modo, Si se gira alrededor del eje de los X, de vector director

${\vec {u}}$

entonces Z aparece bajo la misma forma que Y en la ecuación, es decir con un signo «-»: X² - Y² - Z² = 1.

Reagrupando las coordenadas del mismo signo al inicio de la ecuación, cambiando los signos si hay dos negativos y renombrando las variables para obtener el orden habitual x,y,z, se obtiene una de estas dos ecuaciones:

x² + y² - z² = 1     o     x² + y² - z² = -1
(una hoja)                                  (dos hojas)

Se generaliza estos dos ejemplos así: un hiperboloide es una cuádrica cuya ecuación es, en un sistema de coordenadas adecuado (centrado en el centro de simetría, y cuyos planos son de planos de simetría de la superficie) de la forma:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1\ {\mbox{ (hiperboloide de una hoja) }}\qquad {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=-1\ {\mbox{ (hiperboloide de dos hojas) }}$

Estas superficies se obtienen de las mostradas en ejemplo estirando en la dirección de los x por el factor a, multiplicando las distancias en los y por b, y en los z por c. Es decir que tienen fundmentalmente la misma forma.

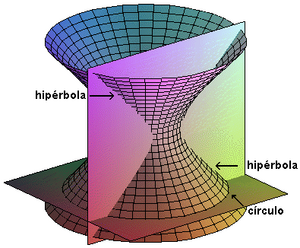
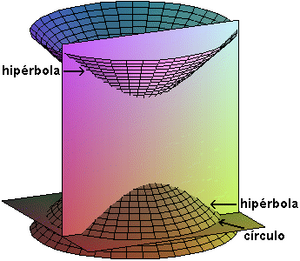
Las figuras siguientes presentan la sección de los hiperboloides, por un plano paralelo a su eje, y otro perpendicular a éste.

La sección por un plano perpendicular al eje (de ecuación z = constante) es una elipse de ecuación

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=constante$

- en las figuras son círculos, lo que corresponde a a = b y a la definición inicial de superficie de revolución.
La sección por un plano vertical es una hipérbola - lo que justifica la apelación de la superficie en el caso general - de distintas orientaciones según los casos. Por ejemplo, un plano vertical de ecuación x = k constante corta el primer hiperboloide según la curva

${\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1-{\frac {k^{2}}{a^{2}}}=k'{\mbox{ constante}}$

, que es la de una elipse.

Referencias

Referencias e información de imágenes pulsando en ellas.