Coordenadas polares

El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto (posición)en el plano esta determinado por un ángulo y una distancia. El sistema de coordenadas polares es especialmente útil en situaciones donde la relación entre dos puntos es mas fácil de expresar en términos de ángulos y distancias; en el sistema de coordenadas cartesiano o rectangular estas mismas relaciones deben ser expresadas mediante fórmulas trigonométricas. Al ser un sistema de coordenadas bidimensional, cada punto dentro del plano se encuentra determinado por dos coordenadas: la coordenada radial y la coordenada angular. La coordenada radial (comúnmente simbolizada por r) expresa la distancia del punto al punto central del sistema conocido como polo (equivalente al origen del sistema Cartesiano). La coordenada angular (también conocida como ángulo polar o ángulo acimutal, y usualmente simbolizado por θ ó t) expresa el ángulo positivo (es decir en sentido anti horario) medido desde el eje polar (usualmente se hace coincidir este con el eje x del sistema cartesiano)

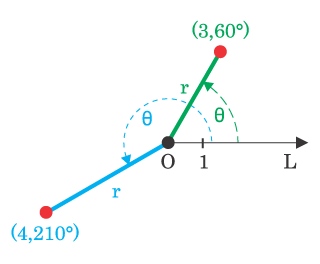
En la figura, se representa un sistema de coordenadas polares en el plano, el centro de referencia, punto O y la línea OL sobre la que se miden los ángulos, en las referencias a los puntos indicando la distancia al centro de coordenadas y el ángulo sobre el eje OL.

• El punto (3, 60º), indica que está a una distancia de 3 unidades de O, medidas con un ángulo de 60º sobre OL.

• El punto (4, 210º)indica que está a una distancia de 4 unidades de O y un ángulo de 210º sobre OL.

Este sistema se emplea en los casos en los que el conocimiento de los ángulos directores sea más práctico que las coordenadas cartesianas. Normalmente, eso sucede cuando la figura o curva a estudiar está definida más claramente por los ángulos sobre los ejes y la distancia al centro de coordenadas, como en las figuras de revolución, en los movimientos giratorios, en las observaciones estelares, etc.

En el sistema de coordenadas polares no hay una función biyectiva entre los puntos del espacio y las coordenadas, dado que:

• el centro de coordenadas está definido por una distancia nula, independientemente de los ángulos que se especifiquen
• un punto definido por un ángulo y una distancia, es el mismo punto que el indicado por ese mismo ángulo más un número de revoluciones completas y la misma distancia

Esta circunstancia debe tenerse en cuenta para evitar confusiones en este sistema de coordenadas.

Coordenadas polares en el plano

En el plano de ejes xy con centro de coordenadas en el punto O se puede definir un sistema de coordenadas polares de un punto M del plano, definidas por la distancia r al centro de coordenadas, y el ángulo $\theta$ del vector de posición sobre el eje x.

Conversión de coordenadas rectangulares a polares

Definido un punto del plano por sus coordenadas rectangulares (x,y), se tiene que las coordenadas polares son:

$\tan \theta ={\frac {y}{x}}$

$r={\sqrt {x^{2}+y^{2}}}$

Conversión de coordenadas polares a rectangulares

Definido un punto en coordenadas polares por su ángulo $\theta$ sobre el eje x, y su distancia r al centro de coordenadas, se tiene:

$x=r\cos \theta \,$

$y=r\sin \theta \,$

Coordenadas polares en el espacio

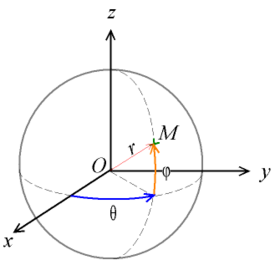
Dado el espacio tridimensional, con centro de coordenadas O y ejes xyz, se puede definir un sistema de coordenadas polares, de modo que un punto del espacio M está definido por dos ángulos directores $\theta ,\varphi$ y la distancia al centro de coordenadas r, donde el primer ángulo $\theta \,$ es el que forma la proyección del vector r sobre el plano xy y el eje x, y el segundo ángulo $\varphi \,$ es el que forma el vector r con el plano xy.

Conversión de coordenadas rectangulares a polares

Definido un punto M en el espacio por sus coordenadas rectangulares (x,y,z), se tiene que:

$\tan \theta ={\frac {y}{x}}$

$\tan \varphi ={\frac {z}{\sqrt {x^{2}+y^{2}}}}$

$r={\sqrt {x^{2}+y^{2}+z^{2}}}$

Conversión de coordenadas polares a rectangulares

Definido un punto en el espacio por sus ángulos directores y la distancia al centro de coordenadas r, se tiene:

$x=r\cos \varphi \cos \theta \,$

$y=r\cos \varphi \sin \theta \,$

$z=r\sin \varphi \,$

Ejemplos

En el plano

Una circunferencia se define en coordenadas polares:por lo tanto

$r(\theta )=radio\,$

Una espiral se define, un caso particular es cuando el radio es proporcional al ángulo:

$r(\theta )=k\theta \,$

donde k es un valor real, da lugar a la Espiral de Arquímedes

Otros ejemplos:

• Espiral logarítmica
• Espiral de Fermat

En el espacio

Las coordenadas polares en el espacio tienen especial interés cuando los ángulos determinan la función como, por ejemplo:

• Hélice (geometría)

Enlaces externos

• FooPlot (herramienta que puede mostrar gráficas de funciones en coordenadas polares)
• Herramienta online para la conversión de coordenadas cartesianas en coordenadas polares y a la inversa
• Gráficas de funciones en coordenadas polares