Inscríbete y crea tu propia colección de obras y artículos
Diferencia entre revisiones de «Primer momento de área»
m (1 revisión) |
m (Texto reemplazado: «\|thumb\|right\|» por «|right|») |
||
| (No se muestran 20 ediciones intermedias de 3 usuarios) | |||
| Línea 1: | Línea 1: | ||
{{+}}El '''primer momento de área''' es una magnitud geométrica que se define para un área plana. Normalmente aparece en el contexto del cálculo de [[viga]]s en ingeniería estructural, en particular la [[tensión]] cortante media dada por la [[Esfuerzo cortante|fórmula de Collignon]], que es proporcional al primer momento de área de una subsección de la [[prisma mecánico|sección transversal]] de la viga. El primer momento de área coincide con el producto del área total multiplicado por la distancia entre el punto considerado al Centroide del área. | |||
==Primer momento de área== | ==Primer momento de área== | ||
Los momentos de primer orden de un área, se designan por la letra ''S'' o ''Q''. Dado un eje o recta se define el primer momento de área de el área <math>A </math> respecto a un eje de ecuación <math>(cos(\alpha)x+sin(\alpha)y)+c = 0</math> viene dado por la integral sobre el área de la distancia al eje fijado:</ | Los momentos de primer orden de un área, se designan por la letra ''S'' o ''Q''. Dado un eje o recta se define el primer momento de área de el área <math>A </math> respecto a un eje de ecuación <math>(cos(\alpha)x+sin(\alpha)y)+c = 0</math> viene dado por la integral sobre el área de la distancia al eje fijado:<br /> | ||
</ | <br /> | ||
:<math>S_{eje} = \int_A \quad d(x,y) \quad dxdy = | :<math>S_{eje} = \int_A \quad d(x,y) \quad dxdy = | ||
\int_A \quad (cos(\alpha)x+sin(\alpha)y+c) \quad dxdy </math> | \int_A \quad (cos(\alpha)x+sin(\alpha)y+c) \quad dxdy </math> | ||
</ | <br /> | ||
Si consideramos coordenadas ''x'' e ''y'' centradas en el | Si consideramos coordenadas ''x'' e ''y'' centradas en el Centro de masas y se calculan los primeros momentos de área respecto a los ejes coordenados, por la propia definición de centro de masas:<br /> | ||
</ | <br /> | ||
:<math>S_x^{CM} = \int_A y \quad dxdy = y_{G}\cdot A = 0</math> | :<math>S_x^{CM} = \int_A y \quad dxdy = y_{G}\cdot A = 0</math> | ||
:<math>S_y^{CM} = \int_A x \quad dxdy = x_{G}\cdot A = 0</math> | :<math>S_y^{CM} = \int_A x \quad dxdy = x_{G}\cdot A = 0</math> | ||
</ | <br /> | ||
Eso implica que para cualquier otro eje que pase por el centro de gravedad de la sección se tiene:</ | Eso implica que para cualquier otro eje que pase por el centro de gravedad de la sección se tiene:<br /> | ||
</ | <br /> | ||
:<math>S_{eje}^{CM} = \int_A \quad (cos(\alpha)x+sin(\alpha)y) \quad dxdy = A(\cos(\alpha)x_{G}+\sin(\alpha)y_{G}) = A(0+0) = 0 </math> | :<math>S_{eje}^{CM} = \int_A \quad (cos(\alpha)x+sin(\alpha)y) \quad dxdy = A(\cos(\alpha)x_{G}+\sin(\alpha)y_{G}) = A(0+0) = 0 </math> | ||
</ | <br /> | ||
El cálculo respecto a un eje cualquiera que no pase por en centro de masas es trivial ya que:</ | El cálculo respecto a un eje cualquiera que no pase por en centro de masas es trivial ya que:<br /> | ||
</ | <br /> | ||
:<math>S_{eje} = \int_A \quad (cos(\alpha)x+sin(\alpha)y+c) \quad dxdy = A \cdot c </math> | :<math>S_{eje} = \int_A \quad (cos(\alpha)x+sin(\alpha)y+c) \quad dxdy = A \cdot c </math> | ||
</ | <br /> | ||
Donde resulta que ''c'' coincide con la distancia de ese eje al centro de gravedad y el resultado anterior es el equivalente del | Donde resulta que ''c'' coincide con la distancia de ese eje al centro de gravedad y el resultado anterior es el equivalente del Teorema de Steiner para el primer momento de área. | ||
===Primer momento de área parcial=== | ===Primer momento de área parcial=== | ||
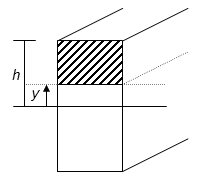
[[ | [[Archivo:FirsMomAr.png|right|205px|Área parcial para el cálculo de la tensión cortante]] | ||
Como se ha visto en la sección anterior el primer momento de área calculado respecto al centro de gravedad de la sección es siempre nulo. Sin embargo, si se considera un área parcial de una sección y se calcula el primer momento de área respecto al centro de gravedad de la sección competa el resultado no es cero. Designaremos a este primer momento de área parcial por la letra <math>Q_y\,</math> y su valor vendrá dado por:</ | Como se ha visto en la sección anterior el primer momento de área calculado respecto al centro de gravedad de la sección es siempre nulo. Sin embargo, si se considera un área parcial de una sección y se calcula el primer momento de área respecto al centro de gravedad de la sección competa el resultado no es cero. Designaremos a este primer momento de área parcial por la letra <math>Q_y\,</math> y su valor vendrá dado por:<br /> | ||
</ | <br /> | ||
:<math>Q_y(y) = \int_{A_p} \bar{y} d\bar{x} d\bar{y} = h_G \cdot A_p </math> | :<math>Q_y(y) = \int_{A_p} \bar{y} d\bar{x} d\bar{y} = h_G \cdot A_p </math> | ||
</ | <br /> | ||
Para una sección rectangular de dimensiones 2''h'' x 2''b'' se tiene:</ | Para una sección rectangular de dimensiones 2''h'' x 2''b'' se tiene:<br /> | ||
</ | <br /> | ||
:<math>Q_y(y) = \int_{-b}^{b} d\bar{x}\int_y^h \bar{y}d\bar{y}= | :<math>Q_y(y) = \int_{-b}^{b} d\bar{x}\int_y^h \bar{y}d\bar{y}= | ||
\frac{h+y}{2}A_p = \frac{b(h^2-y^2)}{2} </math> | \frac{h+y}{2}A_p = \frac{b(h^2-y^2)}{2} </math> | ||
| Línea 36: | Línea 36: | ||
==Segundo momento de área== | ==Segundo momento de área== | ||
Análogamente al primer momento de área se define el segundo momento de área como:</ | Análogamente al primer momento de área se define el segundo momento de área como:<br /> | ||
</ | <br /> | ||
:<math>I_{eje} = \int_A \quad d^2(x,y) \quad dxdy = | :<math>I_{eje} = \int_A \quad d^2(x,y) \quad dxdy = | ||
\int_A \quad (cos(\alpha)x+sin(\alpha)y+c)^2 \quad dxdy </math> | \int_A \quad (cos(\alpha)x+sin(\alpha)y+c)^2 \quad dxdy </math> | ||
</ | <br /> | ||
Que puede expresarse en función de los segundos momentos de área respecto al centro de masas como:</ | Que puede expresarse en función de los segundos momentos de área respecto al centro de masas como:<br /> | ||
</ | <br /> | ||
:<math>I_{eje} = I_{eje}^{CM} + Ac^2 </math> | :<math>I_{eje} = I_{eje}^{CM} + Ac^2 </math> | ||
</ | <br /> | ||
Este último resultado de demostración inmediata se conoce como | Este último resultado de demostración inmediata se conoce como Teorema de Steiner. | ||
==Momentos de área de orden superior== | ==Momentos de área de orden superior== | ||
En general se definen los ''n''-ésimos momento de área de una área plana como las integrales del tipo:</ | En general se definen los ''n''-ésimos momento de área de una área plana como las integrales del tipo:<br /> | ||
</ | <br /> | ||
:<math>m_{eje}(A) = \int_A d^n(x,y) \quad dxdy </math>< | :<math>m_{eje}(A) = \int_A d^n(x,y) \quad dxdy </math> | ||
<br /> | |||
Donde la integral se extiende sobre sobre todo el dominio plano ''A'' de ℝ² y donde la distancia ''r'' es la distancia a un eje contenido en el mismo plano que contiene al área. En particular se definen los dos momentos ''n''-ésimos de área como:</ | Donde la integral se extiende sobre sobre todo el dominio plano ''A'' de ℝ² y donde la distancia ''r'' es la distancia a un eje contenido en el mismo plano que contiene al área. En particular se definen los dos momentos ''n''-ésimos de área como:<br /> | ||
</ | <br /> | ||
:<math>m_x(A) = \int_A y^n \quad dxdy </math> | :<math>m_x(A) = \int_A y^n \quad dxdy </math> | ||
:<math>m_y(A) = \int_A x^n \quad dxdy </math>< | :<math>m_y(A) = \int_A x^n \quad dxdy </math> | ||
<br /> | |||
[[ | [[Carpeta:Resistencia de materiales]] | ||
{{Referencias}} | |||
{{W}} | |||
Revisión actual - 11:17 31 mar 2024
El primer momento de área es una magnitud geométrica que se define para un área plana. Normalmente aparece en el contexto del cálculo de vigas en ingeniería estructural, en particular la tensión cortante media dada por la fórmula de Collignon, que es proporcional al primer momento de área de una subsección de la sección transversal de la viga. El primer momento de área coincide con el producto del área total multiplicado por la distancia entre el punto considerado al Centroide del área.
Primer momento de área
Los momentos de primer orden de un área, se designan por la letra S o Q. Dado un eje o recta se define el primer momento de área de el área respecto a un eje de ecuación viene dado por la integral sobre el área de la distancia al eje fijado:
Si consideramos coordenadas x e y centradas en el Centro de masas y se calculan los primeros momentos de área respecto a los ejes coordenados, por la propia definición de centro de masas:
Eso implica que para cualquier otro eje que pase por el centro de gravedad de la sección se tiene:
El cálculo respecto a un eje cualquiera que no pase por en centro de masas es trivial ya que:
Donde resulta que c coincide con la distancia de ese eje al centro de gravedad y el resultado anterior es el equivalente del Teorema de Steiner para el primer momento de área.
Primer momento de área parcial
Como se ha visto en la sección anterior el primer momento de área calculado respecto al centro de gravedad de la sección es siempre nulo. Sin embargo, si se considera un área parcial de una sección y se calcula el primer momento de área respecto al centro de gravedad de la sección competa el resultado no es cero. Designaremos a este primer momento de área parcial por la letra y su valor vendrá dado por:
Para una sección rectangular de dimensiones 2h x 2b se tiene:
El cálculo de este momento se requiere para el cálculo de la tensión cortante sobre la línea punteada (ver figura) de acuerdo con la fórmula de Collignon-Jourawski.
Segundo momento de área
Análogamente al primer momento de área se define el segundo momento de área como:
Que puede expresarse en función de los segundos momentos de área respecto al centro de masas como:
Este último resultado de demostración inmediata se conoce como Teorema de Steiner.
Momentos de área de orden superior
En general se definen los n-ésimos momento de área de una área plana como las integrales del tipo:
Donde la integral se extiende sobre sobre todo el dominio plano A de ℝ² y donde la distancia r es la distancia a un eje contenido en el mismo plano que contiene al área. En particular se definen los dos momentos n-ésimos de área como:
Referencias
| Referencias e información de imágenes pulsando en ellas. |
| Wikipedia, con licencia CC-by-sa |