Loxodrómica

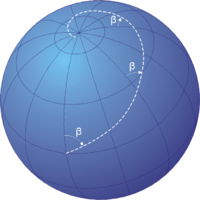
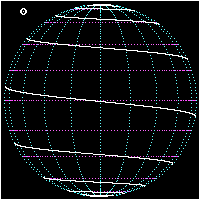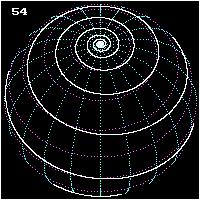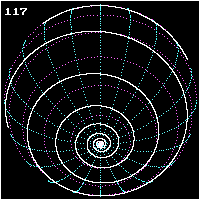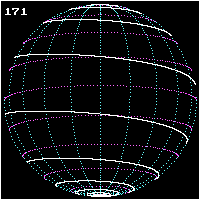
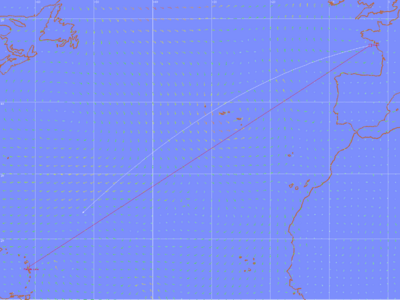
Se denomina loxodrómica o loxodromia (del Griego λοξóς -oblicuo- y δρóμος -carrera, curso-), a la línea que une dos puntos cualesquiera de la superficie terrestre cortando a todos los meridianos con el mismo ángulo. La loxodrómica, por tanto, es fácil de seguir manteniendo el mismo Rumbo marcado por la Brújula. Su representación en el mapa dependerá del tipo de proyección del mismo, por ejemplo en la de Mercator es una recta.

La loxodrómica es junto a la ortodrómica y la isoazimutal, una de las tres líneas que pueden trazarse entre dos puntos cualesquiera de la superficie terrestre.

Pedro Nunes, geógrafo portugués, publicó su descubrimiento en 1546 su Tratado de la navegación, con grandes implicaciones para la navegación. Antes se creía que, marchando sobre la superficie terrestre con un rumbo fijo, es decir, formando un ángulo constante con la meridiana, la línea recorrida era un Círculo máximo o, en otros términos, que un navío que siguiese este derrotero llegaría teóricamente a dar la vuelta al mundo, volviendo al punto de partida. Nunes fue el primero en señalar la falsedad de este concepto tan arraigado, demostrando rigurosamente que, lejos de suceder así, la curva recorrida se va acercando al polo, alrededor del cual da infinitas vueltas sin llegar nunca a él; o, dicho en lenguaje técnico, tiene el polo por punto asintótico.

Gráfico comparativo: