Curva

En matemáticas, el concepto de curva intenta capturar la idea intuitiva de línea continua, de una dimensión, que varía de dirección paulatinamente. Ejemplos sencillos de curvas cerradas son la elipse o la circunferencia, y de curvas abiertas la parábola, la hipérbola o la catenaria. La recta sería el caso límite de una curva de radio infinito.

Definiciones

En geometría, una curva en el n-espacio euclideano es un conjunto ${\mathcal {C}}\subset \mathbb {R} ^{n}$ que es la imagen de un intervalo Ι abierto bajo una aplicación diferenciable $\mathbf {x} \colon \mathrm {I} \to \mathbb {R} ^{n}$, i.e:

${\mathcal {C}}=\{\mathbf {x} (t)\in \mathbb {R} ^{n}\colon t\in \mathrm {I} \}$

donde suele decirse que ($\mathbf {x} ,\mathrm {I}$) es una representación paramétrica o Parametrización de ${\mathcal {C}}$.

Con el objetivo de evitar auto intersecciones, puntos singulares y a los extremos, se define el concepto de curva simple como aquella curva tal que para todo punto p existe un Ω entorno abierto de p para el cual $\Omega \cap {\mathcal {C}}$ admite una representación de clase $C^{k}$ con $k\geq 1$.

El diccionario de la Real Academia Española de la Lengua la define en su página web, de la siguiente manera: 1. f. Geom. La que no es recta en ninguna de sus porciones.

Geometría diferencial de curvas en $\mathbb {R} ^{3}$

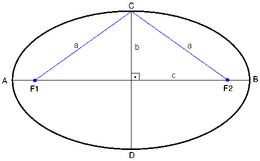
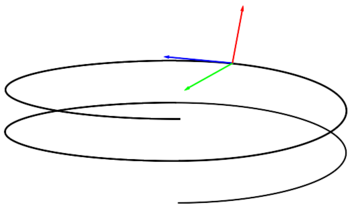
La geometría diferencial de curvas propone definiciones y métodos para analizar curvas simples en el Espacio euclídeo‏‎ tridimensional o, más generalmente, curvas contenidas en variedades de Riemann. En particular, en el espacio euclídeo tridimensional $\mathbb {R} ^{3}$, una curva de la que se conoce un punto de paso y el vector tangente en dicho punto, queda totalmente descrita por su curvatura y torsión. Esta curvatura y torsión pueden estudiarse mediante el llamado triedro de Frênet-Serret, que se explica a continuación.

Vectores tangente, normal y binormal

Dada una curva parametrizada r(t) según un parámetro cualquiera t se define el llamado vector tangente, binormal y normal como:

$\mathbf {t} (t)={\frac {\mathbf {r} '(t)}{\left\Vert \mathbf {r} '(t)\right\|}}$

$\mathbf {b} (t)={\frac {\mathbf {r} '(t)\times \mathbf {r} ''(t)}{\left\Vert \mathbf {r} '(t)\times \mathbf {r} ''(t)\right\|}}$

$\mathbf {n} (t)=\mathbf {b} (t)\times \mathbf {t} (t)$

Estos tres vectores son unitarios y perpendiculares entre sí, juntos configuran un sistema de referencia móvil conocido como triedro de Frênet-Serret. Es interesante que para una partícula física desplazándose en el espacio, el vector tangente es paralelo a la velocidad, mientras que el vector normal da el cambio dirección por unidad de tiempo de la velocidad o aceleración normal.

Referencias

Referencias e información de imágenes pulsando en ellas.