Coordenadas cilíndricas

---

Coordenadas cilíndricas

Las coordenadas cilíndricas son un sistema de coordenadas para definir la posición de un punto del espacio mediante un ángulo, una distancia con respecto a un eje y una altura en la dirección del eje.

El sistema de coordenadas cilíndricas es muy conveniente en aquellos casos en que se tratan problemas que tienen simetría de tipo cilíndrico o acimutal. Se trata de una versión en tres dimensiones de las coordenadas polares de la Geometría analítica plana.

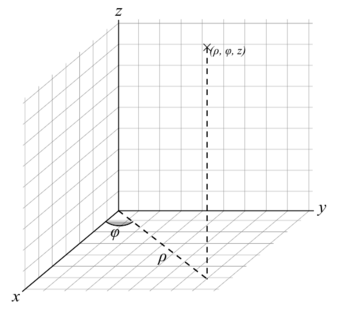
Un punto $P$ en coordenadas cilíndricas se representa por (ρ,φ,$z$), donde:

• ρ: Coordenada radial, definida como la distancia del punto $P$ al eje $z$, o bien la longitud de la proyección del radiovector sobre el plano $XY$
• φ: Coordenada acimutal, definida como el ángulo que forma con el eje $X$ la proyección del radiovector sobre el plano $XY$.
• $z$: Coordenada vertical o altura, definida como la distancia, con signo, desde el punto P al plano $XY$.

Los rangos de variación de las tres coordenadas son

$0\leq \rho <\infty \qquad 0\leq \varphi <2\pi \qquad -\infty <z<\infty$

La coordenada acimutal φ se hace variar en ocasiones desde -π a +π. La coordenada radial es siempre positiva. Si reduciendo el valor de ρ llega a alcanzarse el valor 0, a partir de ahí, ρ vuelve a aumentar, pero φ aumenta o disminuye en π radianes.

Relación con otros sistemas de coordenadas

Relación con las coordenadas cartesianas

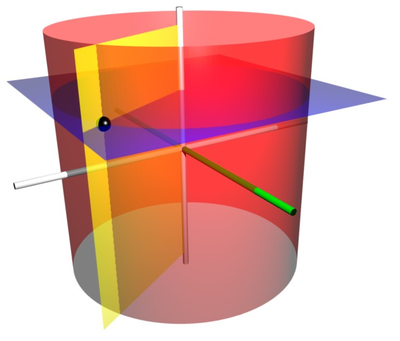
Líneas y superficies coordenadas

Las líneas coordenadas son aquellas que se obtienen variando una de las coordenadas y manteniendo fijas las otras dos. Para las coordenadas cilíndricas, estas son:

• Líneas coordenadas ρ: Semirrectas horizontales partiendo del eje $Z$.
• Líneas coordenadas φ: Circunferencias horizontales.
• Líneas coordenadas $z$: Rectas verticales

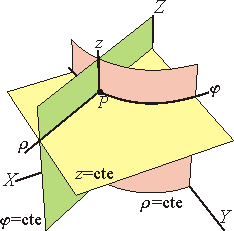
Las superficies coordenadas son aquellas que se obtienen fijado sucesivamente cada una de las coordenadas de un punto. Para este sistema son:

• Superficies ρ=cte.: Cilindros rectos verticales.
• Superficies φ=cte.: Semiplanos verticales.
• Superficies $z$=cte.: Planos horizontales.

Las líneas y superficies coordenadas de este sistema son perpendiculares dos a dos en cada punto. Por ello, éste es un sistema ortogonal.

Base coordenada

A partir del sistema de coordenadas cilíndricas puede definirse una base vectorial en cada punto del espacio, mediante los vectores tangentes a las líneas coordenadas. Esta nueva base puede relacionarse con la base fundamental de las coordenadas cartesianas mediante las relaciones

${\hat {\rho }}=\cos \varphi \,{\hat {x}}+{\rm {sen}}\,\varphi \,{\hat {y}}$

${\hat {\varphi }}=-{\rm {sen}}\varphi \,{\hat {x}}+\cos \,\varphi \,{\hat {y}}$

${\hat {z}}={\hat {z}}$

e inversamente

${\hat {x}}=\cos \varphi \,{\hat {\rho }}-{\rm {sen}}\,\varphi \,{\hat {\varphi }}$

${\hat {y}}={\rm {sen}}\varphi \,{\hat {\rho }}+\cos \,\varphi \,{\hat {\varphi }}$

${\hat {z}}={\hat {z}}$

En el cálculo de esta base se obtienen los factores de escala

$h_{\rho }=1\qquad h_{\varphi }=\rho \qquad h_{z}=1$

Disponiendo de la base de coordenadas cilíndricas se obtiene que la expresión del vector de posición en estas coordenadas es

${\vec {r}}=\rho \,{\hat {\rho }}+z\,{\hat {z}}$

Nótese que no aparece un término $\varphi \,{\hat {\varphi }}$. La dependencia en esta coordenada está oculta en los vectores de la base.

Diferenciales de línea, superficie y volumen

Diferencial de línea

Un desplazamiento infinitesimal, expresado en coordenadas cilíndricas, viene dado por

$d{\vec {r}}=h_{\rho }\,d\rho \,{\hat {\rho }}+h_{\varphi }\,d\varphi \,{\hat {\varphi }}+h_{z}\,dz\,{\hat {z}}=d\rho \,{\hat {\rho }}+\rho \,d\varphi \,{\hat {\varphi }}+dz\,{\hat {z}}$

Diferenciales de superficie

La expresión general de un diferencial de superficie en coordenadas curvilíneas es complicada.

Sin embargo, para el caso de que se trate de una superficie coordenada, $q_{3}={\rm {cte.}}$ el resultado es

$d{\vec {S}}_{q_{3}={\rm {cte}}}=h_{1}\,h_{2}\,dq_{1}\,dq_{2}\,{\hat {q}}_{3}$

y expresiones análogas para las otras dos superficies coordenadas.

En el caso particular de las coordenadas cilíndricas, los diferenciales de superficie son

• ρ=cte: $d{\vec {S}}_{\rho ={\rm {cte}}}=\rho \,d\varphi \,dz\,{\hat {\rho }}$
• φ=cte: $d{\vec {S}}_{\varphi ={\rm {cte}}}=d\rho \,dz\,{\hat {\varphi }}$
• z=cte: $d{\vec {S}}_{z={\rm {cte}}}=\rho \,d\rho \,d\varphi \,{\hat {z}}$

Diferencial de volumen

El volumen de un elemento en coordenadas curvilíneas equivale al producto del Jacobiano de la transformación, multiplicado por los tres diferenciales. El jacobiano, a su vez, es igual al producto de los tres factores de escala, por lo que

$dV=h_{1}\,h_{2}\,h_{3}\,dq_{1}\,dq_{2}\,dq_{3}$

que para coordenadas cilíndricas da

$dV=\rho \,d\rho \,d\varphi \,dz$

Operadores diferenciales en coordenadas cilíndricas

El gradiente, la Divergencia, el Rotacional y el Laplaciano poseen expresiones particulares en coordenadas cilíndricas. Estas son:

• Gradiente

$\nabla \phi ={\frac {\partial \phi }{\partial \rho }}{\hat {\rho }}+{\frac {1}{\rho }}{\frac {\partial \phi }{\partial \varphi }}{\hat {\varphi }}+{\frac {\partial \phi }{\partial z}}{\hat {z}}$

• Divergencia

$\nabla \cdot {\vec {F}}={\frac {1}{\rho }}{\frac {\partial (\rho F_{\rho })}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial (F_{\varphi })}{\partial \varphi }}+{\frac {\partial (F_{z})}{\partial z}}$

• Rotacional

$\nabla \times {\vec {F}}={\frac {1}{\rho }}\left|{\begin{matrix}{\hat {\rho }}&\rho \,{\hat {\varphi }}&{\hat {z}}\\&&\\{\frac {\partial }{\partial \rho }}&{\frac {\partial }{\partial \varphi }}&{\frac {\partial }{\partial z}}\\&&\\F_{\rho }&\rho \,F_{\varphi }&F_{z}\end{matrix}}\right|$

• Laplaciano

$\nabla ^{2}\phi ={\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}\left(\rho {\frac {\partial \phi }{\partial \rho }}\right)+{\frac {1}{\rho ^{2}}}{\frac {\partial ^{2}\phi }{\partial \varphi ^{2}}}+{\frac {\partial ^{2}\phi }{\partial z^{2}}}$

Referencias

Referencias e información de imágenes pulsando en ellas.