Inscríbete y crea tu propia colección de obras y artículos
Sistema de coordenadas
Un sistema de coordenadas es un conjunto de valores y puntos que permiten definir unívocamente la posición de cualquier punto de un Espacio euclídeo o más generalmente Variedad diferenciable.
En física se usan normalmente sistemas de coordenadas ortogonales. Un Sistema de referencia, viene dado por un punto de referencia y un sistema de coordenadas. En Mecánica newtoniana se emplean sistemas de referencia caracterizados por un punto denominado origen y un conjunto de ejes definen unas coordenadas.
Sistemas de coordenadas
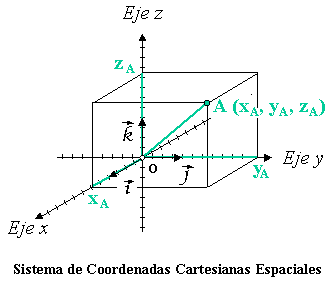
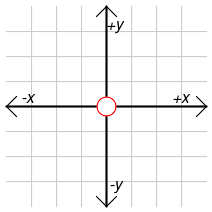
Sistema de coordenadas cartesianas
Un sistema de coordenadas cartesianas se define por dos o tres ejes ortogonales igualmente escalados, dependiendo de si es un sistema Bidimensional o tridimensional. El valor de cada una de las coordenadas de un punto (A) es igual a la Proyección ortogonal del vector de posición de dicho punto () sobre un eje determinado.
Cada uno de los ejes está definido por un Vector director y por el origen de coordenadas. Por ejemplo, el eje x está definido por el origen de coordenadas (O) y un Vector unitario ().
- , cuyo módulo es .
El valor de la coordenada X de un punto es igual a la proyección ortogonal del vector de posición de dicho punto sobre el eje x.
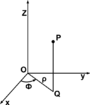
Sistema de coordenadas cilíndricas
El sistema de coordenadas cilíndricas son usadas para parametrizar los puntos de un Espacio euclídeo tridimensional. Este sistema de coordenadas es una generalización del sistema de coordenadas polares plano euclídeo, al que se añade un tercer eje de referencia perpendicular a los otros dos. La primera coordenada es la distancia existente entre el origen y el punto, la segunda es el ángulo que forman el eje y la recta que pasa por ambos puntos, mientras que la tercera es la coordenada que determina la altura del cilindro.
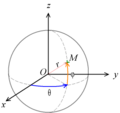
Sistema de coordenadas esféricas
Al igual que las coordenadas cilíndricas, el sistema de coordenadas esféricas se usan en espacios euclídeos tridimensionales. Este sistema de coordenadas esféricas está formado por tres ejes mutuamente perpendiculares que se cortan en el origen. La primera coordenada es la distancia entre el origen y el punto, siendo las otras dos los ángulos que es necesario girar para alcanzar la posición del punto.
Coordenadas geográficas
Este tipo de coordenadas se usa para nombrar puntos sobre una superficie esférica. Hay varios tipos de coordenadas geográficas. El sistema más clásico y conocido es el que emplea la latitud y la longitud, que pueden mostrase en los siguientes formatos:
- DD Decimal Degree (Grados Polares): ej. 49.500-123.500
- DM Degree:Minute (Grados:Minutos.Segundos): ej. 49:30.0-123:30.0
- DMS Degree:Minute:Second (Grados:Minutos:Segundos): ej. 49:30:00-123:30:00
Otro sistema de coordenadas geográficas habitual es el sistema de Coordenadas UTM.
Coordenadas curvilíneas
Un sistema de coordenadas curvilíneos es la forma más general de parametrizar o etiquetar los puntos de un espacio Localmente Euclídeo o Variedad diferenciable (globalmente el espacio puede ser euclídeo pero no necesariamente). Si tenemos un espacio localmente euclídeo M de dimensión m, podemos construir un sistema de coordenadas curvilíneo local en torno a un punto p siempre a partir de cualquier Difeomorfismo que cumpla:
Para cualquier punto q cercano a p se definen sus coordenadas curvilíneas:
Si el espacio localmente euclídeo tiene la estructura de Variedad de Riemann se pueden clasificar a ciertos sistemas de coordenadas curvilíneas en sistema de coordenadas ortogonales y cuando es sistema de coordenadas ortonormales. Las coordenadas cilíndricas y las coordenadas esféricas son casos particulares de sistemas de coordenadas ortogonales sobre el espacio euclídeo .
Cambios de coordenadas
En la resolución de problemas físicos y matemáticos es común la estrategia del cambio de coordenadas. En esencia un cambio de coordenadas supone cambiar las variables de las que depende el problema, a otras coordenadas diferentes en las que el problema puede tener una forma equivalente pero más simple, que permite encontrar la solución con mayor facilidad.
Más formalmente un cambio de coordendas puede representarse por un Difeomorfismo o aplicación biyectiva y diferenciable (con inversa también diferenciable):
Este cambio de variable permite por ejemplo reescribir integrales del siguiente modo:
Para transformar o reescribir ecuaciones diferenciales en términos de las nuevas coordenadas se usan las leyes de tranformación tensorial:
Origen de coordenadas
El Origen de coordenadas es el punto de referencia de un sistema de coordenadas. En este punto, el valor de todas las coordenadas del sistema es nulo. Sin embargo, en algunos sistemas de coordenadas no es necesario establecer nulas todas las coordenadas. Por ejemplo, en un sistema de coordenadas esféricas es suficiente con establecer el radio nulo (), siendo indiferentes los valores de latitud y longitud.
En un sistema de coordenadas cartesianas, el origen es el punto en que los ejes del sistema se cortan.
Enlaces externos
Referencias
| Referencias e información de imágenes pulsando en ellas. |
| Wikipedia, con licencia CC-by-sa |