Inscríbete y crea tu propia colección de obras y artículos
Diferencia entre revisiones de «Momento resistente»
(→Momento resistente flexional: clean up, replaced: ejes principales de inercia → Ejes principales de inercia) |
m (Texto reemplazado: «\|thumb\|(.*)px\|» por «|right|$1px|») |
||
| (No se muestran 10 ediciones intermedias de 3 usuarios) | |||
| Línea 1: | Línea 1: | ||
{{++}} | |||
El '''momento resistente''' es una magnitud geométrica calculable a partir de la forma y dimensiones de una sección transversal que representa la relación entre las tensiones máximas sobre dicha sección transversal y el [[esfuerzo interno|esfuerzo total]] aplicado sobre dicha sección. | El '''momento resistente''' es una magnitud geométrica calculable a partir de la forma y dimensiones de una sección transversal que representa la relación entre las tensiones máximas sobre dicha sección transversal y el [[esfuerzo interno|esfuerzo total]] aplicado sobre dicha sección. | ||
Se lo denomina también ''' Módulo de Inercia''' ó '''Módulo Resistente'''. | Se lo denomina también ''' Módulo de Inercia''' ó '''Módulo Resistente'''. | ||
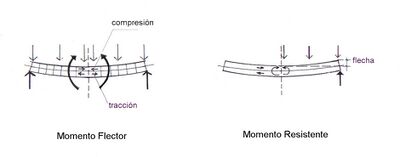
[[Archivo:Momento Flector y Resistente.jpg| | [[Archivo:Momento Flector y Resistente.jpg|right|center|400px|Clicar para ampliar imagen]] | ||
==Momento resistente flexional== | ==Momento resistente flexional== | ||
Para una sección sometida a [[flexión (ingeniería)|flexión]]simple la tensión (σ) viene dada por: | Para una sección sometida a [[flexión (ingeniería)|flexión]]simple la tensión (σ) viene dada por: | ||
| Línea 14: | Línea 15: | ||
\frac{M_y}{W_y} + \frac{M_z}{W_z} </math>||left}} | \frac{M_y}{W_y} + \frac{M_z}{W_z} </math>||left}} | ||
De donde se deduce que los momentos resistentes flexionales vienen dados por: | De donde se deduce que los momentos resistentes flexionales vienen dados por: | ||
{{Ecuación|<math>W_y = \max_z \left| \frac{I_y}{z} \right| \qquad | {{Ecuación|<math>W_y = \max_z \left| \frac{I_y}{z} \right| \qquad | ||
W_z = \max_y \left| \frac{I_z}{y} \right|</math>||left}} | W_z = \max_y \left| \frac{I_z}{y} \right|</math>||left}} | ||
| Línea 20: | Línea 21: | ||
*'''Sección rectangular''' (base ''b'' × altura ''h''): | *'''Sección rectangular''' (base ''b'' × altura ''h''): | ||
{{Ecuación|<math>W_y = \frac{bh^2}{6} \qquad W_z = \frac{b^2h}{6}</math>||left}} | {{Ecuación|<math>W_y = \frac{bh^2}{6} \qquad W_z = \frac{b^2h}{6}</math>||left}} | ||
{{Ref|'''Sección circular maciza''' de radio ''R'':}} | |||
{{Ecuación|<math>W_y = W_z = \frac{\pi R^3}{4}</math>||left}} | {{Ecuación|<math>W_y = W_z = \frac{\pi R^3}{4}</math>||left}} | ||
{{Ref|'''Sección elíptica maciza''' con semiejes ''a'' y ''b'' (''a'' > ''b'')}} | |||
{{Ecuación|<math>W_y = \frac{\pi ab^2}{4} \qquad W_z = \frac{\pi a^2b}{4}</math>||left}} | {{Ecuación|<math>W_y = \frac{\pi ab^2}{4} \qquad W_z = \frac{\pi a^2b}{4}</math>||left}} | ||
| Línea 36: | Línea 37: | ||
{{Ecuación|<math>\sigma_{max} = +\frac{M_x}{J}d_{max} = \frac{M_x}{W_T}</math>||left}} | {{Ecuación|<math>\sigma_{max} = +\frac{M_x}{J}d_{max} = \frac{M_x}{W_T}</math>||left}} | ||
De donde se deduce que para una sección circular maciza o hueca el momento resistente torsional viene dado por: | De donde se deduce que para una sección circular maciza o hueca el momento resistente torsional viene dado por: | ||
{{Ecuación|<math>W_y = \max_d \frac{J}{d} = | {{Ecuación|<math>W_y = \max_d \frac{J}{d} = \frac{J}{R_{ext}}</math>||left}} | ||
Donde ''R<sub>ext</sub>'' es el radio exterior de la sección. | Donde ''R<sub>ext</sub>'' es el radio exterior de la sección. | ||
| Línea 46: | Línea 47: | ||
*'''Sección circular maciza''' de radio ''R'': | *'''Sección circular maciza''' de radio ''R'': | ||
{{Ecuación|<math>W_T = \frac{\pi R^3}{2}</math>||left}} | {{Ecuación|<math>W_T = \frac{\pi R^3}{2}</math>||left}} | ||
{{Ref|'''Sección circular hueca''' con radio exterior ''R<sub>e</sub>'' y radio interior ''R<sub>i</sub>'':}} | |||
{{Ecuación|<math>W_T = \frac{\pi}{2} \frac{R_e^4-R_i^4}{R_e}</math>||left}} | {{Ecuación|<math>W_T = \frac{\pi}{2} \frac{R_e^4-R_i^4}{R_e}</math>||left}} | ||
{{Ref|'''Sección elíptica maciza''' con semiejes ''a'' y ''b'' (''a'' > ''b'')}} | |||
{{Ecuación|<math>W_T = \frac{\pi ab^2}{2}</math>||left}} | {{Ecuación|<math>W_T = \frac{\pi ab^2}{2}</math>||left}} | ||
{{Ref|'''Sección triangular''' equilátera de lado ''L'':}} | |||
{{Ecuación|<math>W_T = \frac{L^3}{20}</math>||left}} | {{Ecuación|<math>W_T = \frac{L^3}{20}</math>||left}} | ||
{{Ref|'''Sección rectangular maciza''' (''b'' × ''a'', ''a'' > ''b''):}} | |||
{{Ecuación|<math>W_T = \frac{k_2}{k_1} \frac{b^2a}{3} \qquad | {{Ecuación|<math>W_T = \frac{k_2}{k_1} \frac{b^2a}{3} \qquad | ||
\begin{cases} | \begin{cases} | ||
k_1 = 1-\cfrac{8}{\pi^2}\sum_{k=0}^\infty \cfrac{1}{(2k+1)^2}\; {\mbox{sech}\cfrac{(2k+1)\pi a}{2b}} \\ | k_1 = 1-\cfrac{8}{\pi^2}\sum_{k=0}^\infty \cfrac{1}{(2k+1)^2}\; {\mbox{sech}\cfrac{(2k+1)\pi a}{2b}} \\ | ||
k_2 = 1-\cfrac{192}{\pi^5}\cfrac{b}{a}\sum_{k=0}^\infty \cfrac{1}{(2k+1)^5}\; | k_2 = 1-\cfrac{192}{\pi^5}\cfrac{b}{a}\sum_{k=0}^\infty \cfrac{1}{(2k+1)^5}\; | ||
{\mbox{tanh}\cfrac{(2k+1)\pi a}{2b}} \end{cases}</math>||left}} | {\mbox{tanh}\cfrac{(2k+1)\pi a}{2b}} \end{cases}</math>||left}} | ||
| Línea 61: | Línea 62: | ||
*'''Sección cerrada de pared delgada''', de espesor constante ''e'' y área media encerrada por la curva media de la sección ''A<sub>m</sub>''. | *'''Sección cerrada de pared delgada''', de espesor constante ''e'' y área media encerrada por la curva media de la sección ''A<sub>m</sub>''. | ||
{{Ecuación|<math>W_T \approx 2eA_m\;</math>||left}} | {{Ecuación|<math>W_T \approx 2eA_m\;</math>||left}} | ||
{{Ref|'''Sección abierta de pared delgada''', como por ejemplo un perfil T o un [[Perfil IPE|pefil H]] ([[perfil doble T]]), aproximable mediante rectángulos alargados de largo ''h<sub>i</sub>'' y espesores constantes ''e<sub>i</sub>'':}} | |||
{{Ecuación|<math>W_T \approx \frac{\frac{1}{3}\sum_j h_je_j^3}{\max_i{e_i}};</math>||left}} | {{Ecuación|<math>W_T \approx \frac{\frac{1}{3}\sum_j h_je_j^3}{\max_i{e_i}};</math>||left}} | ||
| Línea 67: | Línea 68: | ||
[http://ing.unne.edu.ar/pub/e2_cap5.pdf Deducción de varios momentos resistentes de torsión] | [http://ing.unne.edu.ar/pub/e2_cap5.pdf Deducción de varios momentos resistentes de torsión] | ||
[[Carpeta:Resistencia de materiales]] | |||
[[ | {{Terminología}} | ||
{{Referencias}} | |||
{{W}} | {{W}} | ||
{{Clear}} | |||
Revisión actual - 13:18 31 mar 2024
El momento resistente es una magnitud geométrica calculable a partir de la forma y dimensiones de una sección transversal que representa la relación entre las tensiones máximas sobre dicha sección transversal y el esfuerzo total aplicado sobre dicha sección.
Se lo denomina también Módulo de Inercia ó Módulo Resistente.
Momento resistente flexional
Para una sección sometida a flexiónsimple la tensión (σ) viene dada por:
Donde:
- , son las coordenadas de un punto de la sección transversal donde se quieren estudidar las tensiones.
- , son las componentes del momento flector sobre los dos Ejes principales de inercia de la sección transversal.
El valor máximo sobre dicha sección se alcanza para el punto más alejado de la fibra neutra siendo esta tensión máxima:
De donde se deduce que los momentos resistentes flexionales vienen dados por:
Ejemplos
- Sección rectangular (base b × altura h):
| Sección circular maciza de radio R: |
| Sección elíptica maciza con semiejes a y b (a > b) |
Momento resistente torsional
Sección circular maciza o hueca
Para una sección mazica o tubular circular sometida a torsión simple la tensión tangencial (τ) viene dada por:
Donde:
- , son las coordenadas de un punto de la sección transversal donde se quieren estudidar las tensiones.
- , es el momento torsor.
El valor máximo sobre dicha sección se alcanza para el punto más alejado del centro de torsión siendo esta tensión máxima:
De donde se deduce que para una sección circular maciza o hueca el momento resistente torsional viene dado por:
Donde Rext es el radio exterior de la sección.
Otras secciones
Para secciones no-circulares no existe una relación sencilla entre el módulo de torsión y el momento resistente de torsión. El problema con secciones no-circulares presenta alabaeo y a diferencia de lo que sucede en una sección circular las tensiones no son proporcionales a la distancia al centro de la sección. Además las tensiones difieren según la dirección en la que nos separemos del centro al no ser todas la direcciones equivalentes. Para algunas formas concretas como la sección triangular equilátera o la elíptica la función de alabeo es relativamente sencilla de obtener. Sin embargo, la expresión para una sección rectangular resulta bastante más complicado. Para secciones cerradas de pared delgada puede obtenerse una aproximación razonable a efectos de cálculo de forma muy sencilla. En la siguiente sección se dan expresiones para diferentes secciones.
Ejemplos
- Sección circular maciza de radio R:
| Sección circular hueca con radio exterior Re y radio interior Ri: |
| Sección elíptica maciza con semiejes a y b (a > b) |
| Sección triangular equilátera de lado L: |
| Sección rectangular maciza (b × a, a > b): |
Es importante notar que
- Sección cerrada de pared delgada, de espesor constante e y área media encerrada por la curva media de la sección Am.
| Sección abierta de pared delgada, como por ejemplo un perfil T o un pefil H (perfil doble T), aproximable mediante rectángulos alargados de largo hi y espesores constantes ei: |
Enlaces externos
Deducción de varios momentos resistentes de torsión
Referencias
| Referencias e información de imágenes pulsando en ellas. |
| Wikipedia, con licencia CC-by-sa |